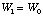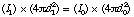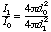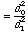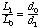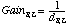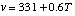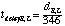Go back to Chapter 2,
skip to Chapter 4
or return to the Index
Chapter 3
SPATIAL PLACEMENT USING ILDS AND ITDS
3.0 The role of interaural level and time differences
3.1 Calculating the ILDs
3.2 ILD implementation
3.3 Calculating the ITDs
3.4 ITD implementation
3.5 Compensation for intrinsic ITDs and ILDs
3.0 The role of interaural level and time differences
By examining the physics underlying the travel of sound waves in air, two location cues become
apparent. As sound radiates outward from a source, the power (and resulting perceived level) drops with
increased distance. If the distances to each ear are unequal, an interaural level difference (ILD) will be
noted. Likewise, since the speed of sound in air is finite, sound which must travel different distances to
each ear will arrive at different times. This is referred to as an interaural time difference, or ITD.
3.1 Calculating the ILDs
The basis for calculating ILDs is the inverse-square law [25]:

where
I is the sound intensity in watts per square meter,
W is the sound power of the source in watts,
d is the distance from the source in meters.
The law assumes that the source is a point source and is radiating uniformly into a free field. The
amount of power flowing through a given solid angle is constant, and allows us to equate the sound power
at two radii:
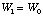
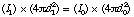
rearranging, we get
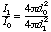
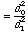
which states simply that the intensity of sound in a free field is inversely proportional to the square of the
distance from the source. While intensity is difficult to measure and manipulate, sound pressure level (SPL)
is relatively easy to deal with. Since SPL is proportional to the square root of the intensity, the inverse-
square law reduces to
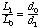
where L is the sound pressure level.
3.2 ILD implementation
The necessity of computing the distance from each ear to the source is now apparent. The distance
formula provides the distance r for the left and right ears. It is tempting to simply use the ratio between the
two to find the ILD. In fact, many systems do process ILDs in this manner. This technique is adequate for
static (non-moving) sources. However, if the sound source is moving radially with respect to the listener, it
is necessary to add another level compensation for the change in distance (the source will appear louder as
it approaches the listener). Another possibility is the use of impulse responses which implicitly include the
level difference. Unfortunately, the source distance is then dictated at the time of HRTF generation and
cannot be accurately compensated by a simple level shift, since the ILD may change at a different rate from
the absolute level. Therefore, it is more reasonable, from a systems perspective, to adjust levels for each ear
individually according to some reference distance at which the sound sources have been recorded. This
results in automatic generation of ILDs and attenuation of sounds as they travel further from the listener's
position, and maintains flexibility to specify distance parameters at run-time.
The level for each ear is adjusted by the reciprocal of the distance to that ear, in meters:
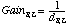
3.3 Calculating the ITDs
ITD calculation depends on the speed of sound in air, and the distance traveled. The speed of sound in
air can be approximated as [26]:
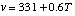
where
v is the speed of sound, in meters per second,
T is the ambient temperature, in degrees Celsius.
This approximation holds true for conditions near room temperature and pressure. The time delay
from the source to the ear is simply the distance divided by the speed of sound.
3.4 ITD implementation
As with ILDs, it is tempting to compute the ITD directly using the difference in path lengths to the
right and left ears or by incorporating it in the HRTF impulse response. Similar problems arise. If the ITD
is computed directly, a separate overall delay must be computed for the time it takes sound to reach the first
ear. This is critical for integration with visual elements. A sound synchronized to a visual event perceived
as several hundred meters away should have an inherent delay; the presentation of sound with the correct
ITD but incorrect absolute delay introduces an anomaly which inhibits the willing suspension of disbelief.
Alternately, if the ITD is intrinsic to the HRTF it reduces accuracy from the filtering function; any delay
simply fills the beginning of the lagging ear's FIR with zeros, reducing the effective filter length without
reducing computational load. A better approach is to compute the delay separately for each ear; ITD's and
absolute delay are computed in a single operation, and both ears benefit from full-length FIR filters.
Because it is impractical and unnecessary to incorporate temperature variations in this project, a static
sound velocity of 346 m/sec was selected for the purposes of computation. The resulting formula is:
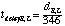
where t is the delay in seconds. The delay in terms of samples is given by multiplying by the sample
rate :

3.5 Compensation for intrinsic ITDs and ILDs
HRTFs recorded with traditional methods (as in Wightman and Kistler [13]) incorporate both a time
delay and a level change, as the impulse source used for measurement is located at some distance d from the
center of the head. To allow source positioning within this radius and a more generalized algorithm, it is
necessary to remove these biases.
Removal of intrinsic ILDs is relatively simple, and involves computing the equivalent level shift for a
source at the HRTF radius (1.43 meters for the set used here) and given angular displacement. This level
shift is then divided out of the ILD shift computed in section 3.1.
ITDs present a more significant challenge, since the delay line must be modified to be anti-causal.
That is, the system must be aware of samples both before and after the current sample being processed. The
maximum number of anticausal samples needed is derived by calculating the longest distance traveled by
the HRTF measurement source. This is equal to the HRTF recording radius plus half the interaural
spacing. For this setup, this is 1.43+0.06 = 1.49 meters. Dividing by the speed of sound gives the delay in
seconds and multiplying by the sample rate provides the maximum embedded delay in samples:

For our 44.1 kHz sample rate, the maximum delay embedded in the HRTF equals 184 samples. Once this
anticausal z-buffer offset is established, the actual HRTF intrinsic delay for a specific source position must
be removed; this is accomplished by subtracting the HRTF equivalent distance from the current source-ear
distance before the ITD calculation described in section 3.4. Note that negative distances are possible, and
resolve to negative delays - hence the need for an anti-causal system.
Continue on to Chapter 4...
Frank Filipanits Jr.
-
franko@alumni.caltech.edu