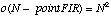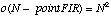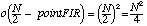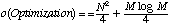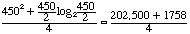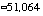Go back to Chapter 4,
skip to Chapter 6
or return to the Index
Chapter 5
FIRST CUT OPTIMIZATION: BAND-LIMITED SOURCES
5.0 Real-world sources
5.1 Bandwidth identification
5.2 Algorithm modification
5.0 Real-world sources
By examination, it is evident that in current auralization algorithms, the computation time is
independent of the characteristics of the source. A complex sound requires the same processing time as a
simple sound, or even a period of silence. It is here we find the first optimization to explore: source-
dependent algorithms.
In auralization systems, a great deal of effort is given to accurate localization of sound sources. Rarely,
however, are such systems called upon to place a broad bandwidth sound. When such occasions do occur, it
is questionable whether pinpoint spatial accuracy is necessary. As an example, consider that most naturally
occurring sounds which emanate from a single point in space (speech, animal vocalizations, etc.) are
limited to a relatively small bandwidth, typically a few thousand Hertz. Sources which maintain large
bandwidth for an extended period of time (such as an orchestra) produce sound from numerous spatial
positions, presenting a diffuse general perception of location. There are some sounds, such a drum, which
nominally have a large bandwidth yet present a localized origin. On further examination, however, it is
apparent that the wide spectral content attributed to such sounds are primarily due to the impulse caused by
a sharp attack transient. Once this transient has passed, the sound settles into a more band-limited range.
The following algorithm is a first attempt at dynamic allocation of resources to match the spectral content
and psychoacoustic "importance" of source signals.
5.1 Bandwidth identification
There are several methods available to identify spectral content in the upper frequency ranges. One
direct approach is to implement an FFT and evaluate the magnitude response in the high frequencies.
Another approach is to use a high-pass time domain filter, and evaluate the magnitude of the remaining
signal. For this project, the FFT approach was adopted. A 256-point FFT was computed every 4096
samples to re-evaluate the bandwidth of the signal. The computation interval of this evaluation is open to
manipulation; it exerts an direct effect on the execution time of the algorithm. However, decreasing the rate
at which frequency snapshots are taken will reduce the system's ability to react quickly to changes in
spectral content.
5.2 Algorithm modification
Once the bandwidth of the signal is known, the algorithm switches between two states. The first state,
when the bandwidth of the signal is high, operates at a full 44.1 kHz sampling frequency but uses a 225
point approximation of the HRTF, effectively halving the "accuracy" of the filter, while also reducing our
computation by half. The second state, for low bandwidth signals, cuts the sampling frequency in half (only
processes every other incoming signal), which results in a 225 point sub-sampled HRTF. The output uses
linear interpolation to upsample back to the original frequency. Because the signal was determined to have
little high-frequency content, the aliasing introduced by this sample rate conversion was negligible.
The overall result of this optimization is a reduction in computation by nearly a factor of four (halving
the length of an FIR quarters the time required to process it) at a cost of a FFT performed at adjustable
intervals. Examining the complexity of the algorithms:
A straight N-point FIR convolution is of order
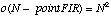
Cutting the resolution in half results in order
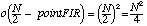
The M-point FFT adds a MlogM term every 4 cycles, so the total order is
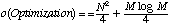
Since M and N are known for this case (M = 256, N=450), we can directly compute the approximate
number of operations for each algorithm. For the straight convolution, the number of operations needed to
process 450 samples is

For the optimized algorithm, the necessary number of operations drops to
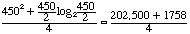
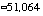
which is very nearly a factor of four. The implications of this savings are tremendous; four times the
number of sources may be computed with the same resources, or three indirect reflections may be computed
for each source (see section 8.2).
Continue on to Chapter 6...
Frank Filipanits Jr.
-
franko@alumni.caltech.edu